平衡树之红黑树

在二叉搜索树文章中提到了最坏情况，这种情况是不能接受的，例如在游戏中的战力值排行榜，数值并不是那么随机，所以更期望在一颗含有N个节点的树中，树的高度为~lgN， 这样就能保证所有查找都能在~lgN次比较内结束

在谈红黑树之前先了解一下2-3树，下图是一颗2-3树

从图中看出，一个2节点含有一个键两条链接，一个3节点含有两个键三条链接，一颗完美平衡的2-3查找树种的所有空链接到根节点的距离都应该相同

2-3树的插入

---

2-3树的插入操作可以简单理解为以下步骤：

1. 2节点
2. 3节点
3. 4节点
4. 拆分4节点为3个2节点

以下列情况说明插入过程

• 向2节点插入新键

  发生如下步骤：

  1. 插入新键
  2. 比根节点的最小值小则向左插入（比根节点的最大值大向右插入）（介于根节点的最小值和最大值之间向中间插入）
  3. 直到找到一个节点（不要忘了我们的前提是：假设这个节点是个2节点）
  4. 向这个2节点插入这个新键，则这个2节点变成3节点

  如下图：

  

• 向一个父节点为2节点的3节点中插入新键

  发生如下步骤：

  1. 插入新键
  2. 比根节点的最小值小则向左插入（比根节点的最大值大向右插入）（介于根节点的最小值和最大值之间向中间插入）
  3. 直到找到一个节点（不要忘了我们的前提是：假设这个节点是个3节点）
  4. 向这个3节点插入这个新键，则这个3节点变成4节点
  5. 拆分这个4节点，将中间值移入父节点（不要忘了我们的前提是：假设这个父节点是个2节点），这个父节点的中间链接指向这个4节点的最小值，右链接指向这个4节点的最大值

  如下图：

  

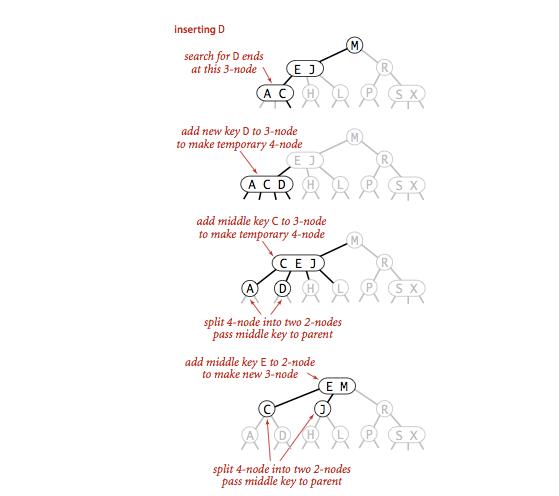
• 向一个父节点为3节点的3节点中插入新键

  发生如下步骤：

  1. 插入新键
  2. 比根节点的最小值小则向左插入（比根节点的最大值大向右插入）（介于根节点的最小值和最大值之间向中间插入）
  3. 直到找到一个节点（不要忘了我们的前提是：假设这个节点是个3节点）
  4. 向这个3节点插入这个新键，则这个3节点变成4节点
  5. 拆分这个4节点，将中间值移入父节点，把最大值和最小值拆分成两个2节点
  6. 这个父节点是个3节点（不要忘了我们的前提是：假设这个父节点是个3节点），按照第5步拆分这个父节点，父节点拆分出来的最小值节点的左右链接指向其子节点拆分出来的最大值和最小值， 父节点拆分出来的最大值节点的左右链接指向其中间节点和右节点
  7. 父节点拆分出来的中间值继续传递给这个父节点的父节点，直到遇到一个2节点

  如下图：

  

上述插入情况中把一个4节点拆分这个过程并不会影响有序性、平衡性。将4节点中的中间值不断的向上传递时，如果最后传递到了根节点，当根节点是3节点那么触发拆分，此时树的高度+1，所以 当根节点被拆分为3个2节点时，所有的空链接到根节点的路径长度+1，和普通的二叉搜索树不同的是：二叉搜索树是由上向下生长，2-3树是由下向上生长

2-3树的插入、删除需要考虑的情况很多，实现复杂，红黑树的实现比2-3树要简单，同时又能达到消除二叉搜索树所带来的最坏情况

红黑树

---

红黑树的特性：

• 红链接均为左链接
• 没有任何一个节点同时和两条红链接相连
• 任意空链接到根节点的路径上的黑链接数量相同，即该树是完美黑色平衡的
• 根节点为黑色的
• 如果将红链接画平，那么所有的空链接到根节点的距离都将是相同的
• 如果将被红链接相连的两个节点合并为一个节点，将会得到一颗2-3树
• 红黑树既是二叉搜索树，也是2-3树

在插入操作中，新节点被标记为红色，这样就会导致两个问题：

• 可能出现右链接是红色
• 两条连续的红链接

解决上述出现的问题，需引入左旋转操作、右旋转操作、变色操作等，总结下来，插入操作过程中要验证并操作的是：

• 如果右子节点是红色的而左子节点是黑色的，进行左旋转
• 如果左子节点是红色的且它的左子节点也是红色的，进行右旋转
• 如果左右子节点都是红色的，进行颜色转换

红黑树代码

---

结合红黑树的特性及插入操作理解一下代码实现，完整的代码实现可以参考github上的代码，最复杂的是它的删除操作，结合算法书中的删除操作介绍，我也是看的云里雾里的， 但是各人觉得相对于使用红黑树来讲，能不能理解删除操作不是最重要的，最重要的是我们能利用红黑树解决什么样生产中的问题，但是总有面试官问道删除操作，我只能说记不住，一次的代码实现终身复用， 又何必记住其内部细节，只要记住红黑树能解决什么问题就可以了

红黑树的代码实现还提供了二叉搜索树实现代码没提供的一些接口，例如是否是搜索树等，同时写了一个对10W个节点的插入操作测试代码，并打印出了这个操作所消耗的毫秒数， 主要是描述了游戏中角色战斗力变化引起的排名变化

红黑树在实际生产中可以用在排行榜，符号表，例如游戏中的战力排行榜，10W个角色的实时排行完全没有问题，还可以做有序符号表

红黑树的特性

---

对于插入、查询等操作（除了遍历、范围查找除外）都能保证操作的运行时间为对数级别

无论键的插入顺序如何，红黑树都几乎是完美平衡的，一颗大小为N的红黑树的高度不会超过2lgN。红黑树的最坏情况是它所对应的2-3树中构成最左边的路径节点全部都是3节点，其余均为2节点，所以最左边的路径 长度是只包含2节点的的路径长度lgN的两倍，虽然这种情况是可能的，但是并不容易构造出来

同时红黑树的一个重要特性是：一颗大小为N的红黑树中，根节点到任意节点的平均路径长度为~lgN

我们可以再次完善二叉搜索树文章中的性能表：

算法	最坏情况下运行时间的增长数量级（N次插入后）查找操作	最坏情况下运行时间的增长数量级（N次插入后）插入操作	平均情况下运行时间的增长数量级（N次插入后）查找操作	平均情况下运行时间的增长数量级（N次插入后）插入操作	有序
二分查找（有序数组）	lgN	N	lgN	N/2	是
二叉树查找（二叉搜索树）	N	N	1.39lgN	1.39lgN	是
红黑树	2lgN	2lgN	lgN	lgN	是