几种二叉树

• 树

  

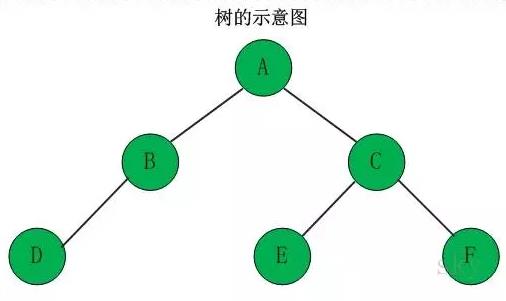
  树是一种非线性数据结构，它是由n（n>=0）个有限节点组成一个具有层次关系的集合

  特点:

  • 每个节点有零个或多个子节点
  • 没有父节点的节点称为根节点
  • 每一个非根节点有且只有一个父节点
  • 除了根节点外，每个子节点可以分为多个不相交的子树

  术语：

  • 结点的度：结点拥有的子树的数目，图中结点c的度为2
  • 叶子：度为零的结点，图中D、E、F都是叶子结点
  • 树的度：树中结点的最大的度，图中结点c的度最大为2，因此树的度为2
  • 层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1
  • 树的高度：树中结点的最大层次，图中树的高度为3。
  • 无序树：如果树中结点的各子树之间的次序是不重要的，可以交换位置
  • 有序树：如果树中结点的各子树之间的次序是重要的, 不可以交换位置
  • 森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林

• 二叉树

  二叉树是每个节点最多有两个子树的树结构。它有五种基本形态：二叉树可以是空集；根可以有空的左子树或右子树；或者左、右子树皆为空

  二叉树的性质：

  • 二叉树第i层上的结点数目最多为 2{i-1} (i≥1)

  • 深度为k的二叉树至多有2{k}-1个结点(k≥1)

  • 包含n个结点的二叉树的高度至少为log2(n+1)

  • 二叉树中,设叶子结点数为n0，度为2的结点数为n2，则n0=n2+1

• 满二叉树

  

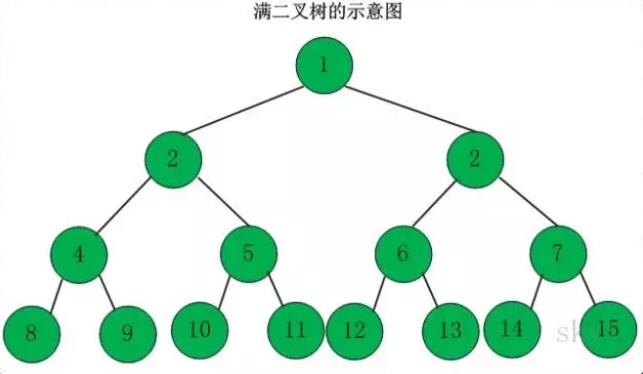
  高度为h，并且由2{h} –1个结点的二叉树，被称为满二叉树，满二叉树的结点的度要么为0（叶子结点），要么为2（非叶子结点）

• 完全二叉树

  

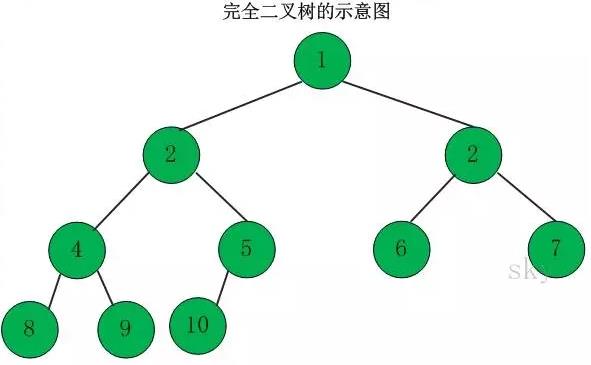
  一棵二叉树中，只有最下面两层结点的度可以小于2，并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树

  特点：

  叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。显然，一棵满二叉树必定是一棵完全二叉树，而完全二叉树未必是满二叉树

• 二叉搜索树

  

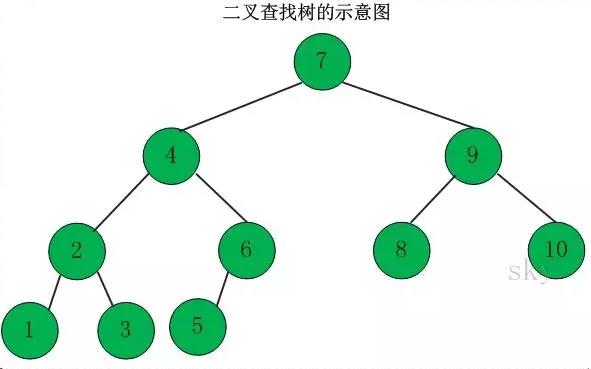
  • 二叉搜索树的左孩子比父节点小，右孩子比父节点大

  • 中序遍历可以让结点有序